摘 要:大数据空间分析是CyberGIS的重要方面。如何利用现有的网络基础设施(如大规模计算集群)对大数据进行并行分布式空间分析仍然是一大难题。提出一种基于MapReduce的空间权重创建方法。该方法依托Hadoop框架组织计算资源,基于MapReduce模式从大规模空间数据集中高效创建出空间权重:大空间数据首先被分为多个数据块,然后将映射器分布给计算集群中的不同节点,以便在数据中寻找出空间对象的相邻对象,最后由约简器从不同节点处收集相关结果并生成权重文件。利用Amazon公司弹性MapReduce的Hadoop框架,从人工空间数据中创建基于邻近概念的权重矩阵进行仿真,实验结果表明,本方法的性能优于传统方法,解决了大数据的空间权重创建问题。
关键词:大数据空间分析;MapReduce;空间权重;附近邻居;可扩展性
引言
大空间数据的出现产生了一些新颖而又颇具挑战性的科学问题[1,2],如空间数据的多尺度表达、基于服务质量保证的空间数据互操作等。为此,人们提出了CyberGIS[3]框架,通过提供一种空间中间件来利用当前网络基础设施(CI)所具有的强大计算资源(如高性能云计算[4,5])来解决这些问题。该框架将空间数据操作、地理可视化、空间模式检测、空间过程建模和空间分析等分布式地理处理组件,无缝地集成为一种可以高效利用CI基础设施计算能力的空间中间件。在这些分布式空间处理组件中,可以解决大空间数据问题的并行空间分析方案是网络GIS系统的重要组件[6]。空间分析过程包括数据预处理、可视化、勘查、模型规格、估计和验证[7]。传统的空间分析数据结构和算法以桌面计算机架构为基础,且只限于桌面计算机架构。鉴于内存空间和计算能力有限,无法用于大空间数据的空间分析中[8,9]。因此,有必要设计和开发一种可展的网络GIS系统平台,为高效的空间分析提供支持。
本文重点研究大数据空间分析时的空间权重生成问题。空间权重代表了空间对象的地理相关性,因此是空间分析的重要方面。空间权重矩阵广泛应用于空间自相关和空间回归等多种空间分析算法中[10,11]。空间权重生成问题主要是指从空间数据中提取出空间相邻信息(邻近权重)和空间距离(距离权重)等空间结构。然而,传统的空间权重生成算法[12,13]基于本地硬件(如CPU、内存和硬盘),性能受限,无法用于处理超大规模空间数据集。因此,本文提出一种基于MapReduce的空间权重创建算法,利用大空间数据创建邻近空间权重。与传统的权重创建算法不同,该方法运行于MapReduce模式下:映射器分布于计算集群中,可并行搜索附近邻居,然后约简器收集结果,进而生成权重矩阵。
1、基于MapReduces 的空间权重生成
1.1 空间权重
空间权重是空间分析(如空间自相关测试、空间回归)的重要方面,需要进行空间结构表示。空间特征的空间结构往往描述为一个n行n列空间权重矩阵W(n表示几何特征量)。如果用featurei和featuej表示为相邻特征,则单元值wij≠0。对于近邻权重矩阵,wij的值要么为1(featurei和featuej相邻),要么为0(featurei和featuej不相邻)。本文重点研究近邻权重生成问题。将一个点定义为两个坐标构成的数组:point=(x,y),将一个多边形定义为M 个点构成的集合:polygon={point1,point2,…,pointM}。对一个包含n个多边形的空间数据集,DS={polygon1,polygon2,…,polygonN},构建一个基于邻近概念的权重矩阵W,就是要对DS中的每个多边形polygoni,i∈[1,N]寻找出所有的相邻多边形。有三种类型的邻近概念可确定权重矩阵中的数值分布:a)rook型邻近(相邻多边形必须共享一条边);b)bishop型邻近(相邻多边形需要共享一个角);c)queen型邻近(相邻多边形要么共享一条边要么共享一个角)
传统的邻近权重矩阵生成算法(如GeoDa[12] 和PySAL[13])利用几何特征来确定两个多边形有没有共享边或共享顶点。如果通过比较所有多边形对的顶点或边缘来确定邻近关系,则这一过程的计算成本太大,时间复杂度为O(n2)。如果对这些几何形状编制空间索引,则在搜索候选相邻多边形时的时间复杂度下降为O(logN)。然而,此时需要额外比较候选和目标几何形状间的原始点或边,以便确定两个几何形状是否相邻。此外,这些算法需要计算机能够将所有几何形状载入内存。因此,无法从超大规模空间数据集中生成邻近权重。
为此,本文提出一种基于Hadoop的MapReduce算法(见算法1),可从超大规模空间数据集中创建邻近权重。该算法基于如下策略:根据多边形包含的顶点和边来对多边形的情况进行汇总。如果两个多边形中出现同一个点/边,则这两个多边形应该是queen型邻近多边形。为了清晰描述本文算法,本文结合queen邻近权重的创建来描述MapReduce算法。该算法依照相同的汇总思路经过简单更改后即可用于rook或bishop邻近权重的创建。为了利用多个计算机节点实现map任务的并行化,Hadoop将会把数据平均分为多个数据块,每个数据块由一个计算机节点处理。在每个节点上,映射器为每个顶点创建一个字典,并将相关多边形添加到数据集中。Hadoop系统将会着眼于约简阶段的计算任务,对所有计算机节点创建的字典进行混洗排序。约简器将会根据键(顶点)对这些字典进行融合。所有字典中具有相同键值的邻近多边形组成的集合或数值,经过融合后生成邻近权重文件。下一节将对算法1的映射和约简过程进行具体介绍。

1 Mapreduces过程
1.2.1 映射
映射的主要目的是利用顶点创建一个{keyvalue}字典对象作为键,同时创建包含该顶点的一组多边形作为值。该算法首先从Hadoop系统的标准输入中读取数据。逐行处理数据。每行表示多边形的几何信息,且以逗号分隔:polyid,point1,point2,…,pointN。这些信息将被解析并存储于poly_polygon_
dict字典中。当映射器处理完数据后,将会对poly_polygon_dict字典中的所有值进行迭代,为约简器准备(keyvalue)数据。因为poly_polygon_dict中的值表示共享相同键(顶点)的多边形,因此认为它们相邻。然后,映射器将键—值对{polygon:neighbor_polygon}写为约简器的相邻信息。
1.2.2 约简
Hadoop系统将会监测和采集所有映射器的输出。一旦映射任务的进度达到系统配置或用户指定阈值,则Hadoop系统将会启动约简任务。约简任务分为混洗、排序和约简三步。在混洗步骤,Hadoop系统对映射输出进行混洗并将映射输出转移到约简器作为输入。在下一个排序步骤中,将会根据{polyid:neighbor_poly_d}字典中多边形主ID(键)对映射输出进行排序。混洗和排序步骤同时进行,以保证每个约简器的输入均被正确排序。在约简步骤中,运行算法2中定义的算法以并行生成每个约简器的权重文件内容。
1.2.3 生成邻近权重文件
因为每个约简器只将其输入写入本地磁盘,所以需要一个专门的融合步骤将所有单个结果进行融合,以生成一个有效的权重文件。本文采用Hadoop平台提供的分布式拷贝工具
(DistCp),来完成MapReduce模式下的融合任务。为了加快融合任务的速度,对约简器做适当配置,将其输出压缩为GNUzip格式,于是数据服务器和计算节点间的数据传输速度加快,且压缩后的文件可直接串联。
算法2 邻近权重生成时的约简算法
1 current_master_poly←None
2 current_neighbor_set←set()
/系统输入:{polyid:neighbor_poly_id}/
4 forline∈sys.stdindo
5 neighbors←line.split()
6 temp_master_poly←neighbors[0]
7 temp_neighbor_poly←None
8 ifneighbor.length>0then
9 temp_neighbor_poly=neighbors[0]
10 end
11 ifcurrent_master_poly≡temp_master_polythen
12 iftemp_neighbor_poly≠Nonethen
13 current_neighbor_set
.add(temp_neighbor_poly)
14 end
15 else
16 ifcurrent_master_poly≡Nonethen
17 ifneighbor_poly≠Nonethen
18 Current_neighbor_set←set()
19 else
20 current_neighbor_set←set([neighbor_poly])
21 end
22 else
23 WriteWeightsFilecurrent_master_poly,current_neighbor_set
24 end
25 end
26 end
/在需要情况下处理最后一行/
/ 将GAL结果写入输出权重文件中/
28 num_neighbors←current_neighbor_set.length()
29 printcurrent_master_poly,num_neighbors
30 printcurrent_neighbor_set.items()
31 end
2、 仿真实验
2.1样本数据集
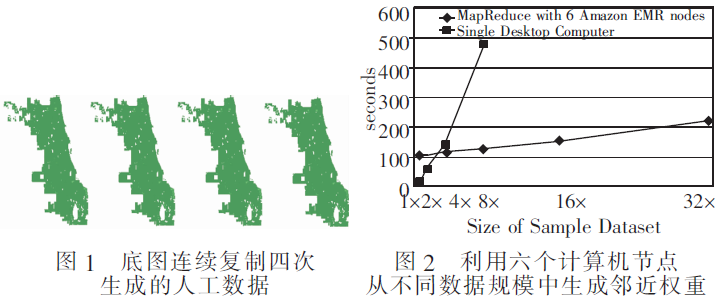
本文实验使用的底图为美国芝加哥市的地块数据。该地块数据包含592521个多边形。为了模拟大规模数据集,利用该底图创建人工大数据:人工多次复制该底图,然后并排放到
一起,生成一个大型人工底图。例如,图1即为4倍于原始数据且含有2370084个多边形的数据图。本文实验中创建的最大规模数据为32倍于原始数据、含有18960672个多边形的数据。整个数据集包括原始数据的1、2、4、8、16和32倍数据。
2.2 测试系统
本文选择Amazon弹性MapReduce(EMR)服务(http://aws.amazon.com/)来创建一个Hadoop测试系统。AmazonEMR服务提供了一种易于使用的可定制Hadoop系统。采用Amazon提供的Hadoop缺省配置。选择运行于AmazonEMR上、节点数量为1~18个节点的“C3ExtraLarge(C3.xlarge)”类型计算机实例集群。除了计算机集群外,Hadoop系统运行时还通过一个主节点来监测所有计算机实例并与所有计算机实例进行通信。C3.xlarge节点的配置包括7.5GB内存,14核(4核×3.5个单元)CPU,80GB(2×40GBSSD),64位操作系统和500Mbps中等网速。除了Hadoop测试系统外,还在一台单机上测试了相同的MapReduce算法,单机配置如下:2.93GHz8核CPU,16GB内存,100GB硬盘,64位操作系统。
结果
为了测试本文MapReduce性能,利用python语言来实现一个桌面版本及通过Hadoop的流式管道功能运行另外一种Hadoop版本。第一个实验是在一台测试单机上运行MapReduce算法。该算法从不同数据规模中生成邻近权重的运行时间,如图2所示。可以看到,随着数据规模的增长,本文算法的运行时间也在增加。该算法的复杂度为O(N),在处理16倍的数据集(9,480,338个多边形)时达到最大计算能力。
第二个实验是在AmazonEMRHadoop系统上运行MapReduce算法。首先,对包含一个主节点和6个C3.xlarge节点的Hadoop系统进行配置,分别测试1、2、4、8、16和32倍数据时的算法性能。该算法从不同数据规模中生成邻近权重的运行时间,如图2所示。因为Hadoop需要花费额外时间传递程序及与运行节点通信,所以如果数据集为原始数据的4倍以下(大约2百万个多边形),则运行时间慢于桌面计算机上运行相同程序所需时间。然而,数据集越大,该算法在Hadoop系统上的
性能越高。例如,对于8倍数据,算法在Hadoop上的完成时间为167s,其运行时间远快于桌面计算机(482.67s)。此外,运行时间呈线性增长,表明本文算法随着数据规模的增长具有良好的可扩展性。
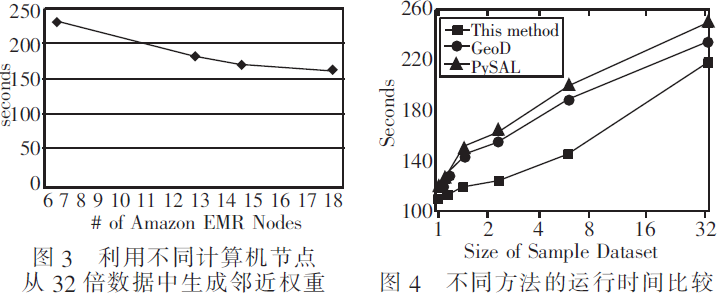
在后续测试中,本文创建带有6、12、14、18个计算机节点的不同Hadoop系统,以便利用32倍数据创建邻近权重。运行时间如图3所示。利用Hadoop中的18个计算机节点,可在163s内生成32倍数据的邻近权重,这是本文在所有测试中获得的最优性能。在图3中,当计算机节点数量增多时,运行时间没有线性下降。这一现象是合理的,因为当计算节点数量增多时,需要额外时间在Hadoop系统内进行通信。
为了进一步体现本文方法的优越性,比较本文方法与传统的邻近权重矩阵生成算法GeoDa[12]和PySAL[13]从不同数据规模中生成邻近权重的运行时间,实验结果如图4所示。可以看到,随着数据规模的增加,不同方法的运行时间都在显著增加。但总的来说,本文方法的性能更优,从1~32倍数据,本文方法的运行时间相比于GeoD和PySAL平均降低了约1415%和17.64%。仔细分析其原因可知,这主要是因为GeoD和PySAL需要计算几何特征间的距离,这种基于距离的计算方法容易受
到数据规模和数据分布的影响,另外GeoD和PySAL主要基于本地硬件,随着数据规模的增加,它们的性能严重受限,因此运行时间较长。而本文方法基于邻近概念来创建空间权重,充分利用了空间对象的地理相关性,通过MapReduce模式避免了不必要的搜索操作,因此节省了时间。
3、 结束语
本文对大数据空间分析时的空间权重
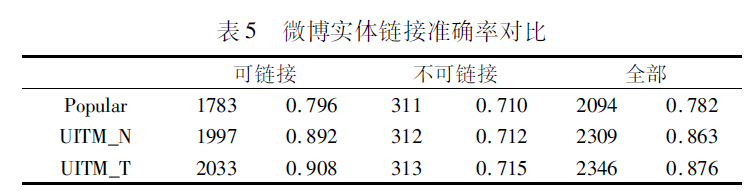
从表5中可以看出,相比基于流行度的方法,两个UITM都取得了较好的结果,充分说明了建模用户兴趣对微博实体链接的重要性。同时,还可以看出,UITM_T相比UITM_N在准确率上也有所提高,证明了考虑用户兴趣传播可以促进实体的链接。然而,对于NIL问题,UITM并没有取得明显提高。NIL问题可以看成是分类问题,UITM等图模型并不适合这样的问题。因此,UITM较好地利用了用户兴趣来提升微博数据的语义,在实体链接准确率,尤其是对可链接名称的实体链接,有了较大提高。
结束语
本文提出了一种基于用户兴趣的微博实体链接方法,解决微博内容较短、歧义较大的问题。该方法首先利用条件独立主题模型训练实体与上下文词汇的语义关联,然后提出了用户兴
趣主题模型UITM,并在真实数据集上进行了实验和分析,取得了87.6%的准确率,实验结果表明UITM通过对用户兴趣的建模丰富了微博的语义,得到了更高的实体链接准确率。然而,由于现有数据集的限制和数据集标注的困难,本文并没有在更大的数据集上进行测试,因此,在未来的研究工作中将进一步对该方法进行测试和改进,使该方法更加实用化。
参考文献:
[1] ShenWei,WangJianyong,HanJiawei.Entitylinkingwithaknowledgebase:issues,techniques,andsolutions[J].IEEE TransonKnowledgeandDataEngineering,2014,27(2):443460.
[2] 邢富坤.基于维基百科的领域实体发现研究[J].计算机应用研究,2015,32(2):347350,367.
[3] 姚宇峰.一种新的重名消解算法在保险领域中的应用研究[J].计生成问题进行研究,提出一种MapReduce算法。该算法利用AmazonEC2云计算平台等高性能计算资源,可为大空间数据(约1.9亿个多边形)生成权重文件,解决了大空间数据的邻近权重生成问题。仿真实验结果表明,本文算法的性能优于传统的以桌面计算机架构为基础的方法。
参考文献:
[1] 吴烨,陈荦,熊伟,等.面向高效检索的多源地理空间数据关联模型[J].计算机学报,2014,37(9):19992010.
[2] GoodchildMF.Whosehandonthetiller?RevisitingspatialstatisticalanalysisandGIS[M]//PerspectivesonSpatialDataAnalysis.Berlin:Springer,2010:4959.
[3] WangShaowen.ACyberGISframeworkforthesynthesisofcyberinfrastructure,GIS,andspatialanalysis[J].AnnalsoftheAssociationofAmericanGeographers,2010,100(3):535557.
[4] 刘荣华,魏加华,翁燕章,等.HydroMP:基于云计算的水动力学建模及计算服务平台[J].清华大学学报:自然科学版,2014,54(5):575583.
[5] YuLian,TsaiW T,WeiXin,etal.Modelingandanalysisofmobilecloudcomputingbasedonbigraphtheory[C]//Procofthe2ndIEEEInternationalConferenceonMobileCloudComputing,Services,andEngineering.2014:6776.
[6] WangShaowen,AnselinL,BhaduriB,etal.CyberGISsoftware:asyn
theticreviewandintegrationroadmap[J].InternationalJournalof
GeographicalInformationScience,2013,27(11):21222145.
[7] AnselinL,ReySJ.SpatialeconometricsinanageofCyberGIScience
[J].InternationalJournalofGeographicalInformationScience,
2012,26(12):22112226.
[8] 关丽,吕雪锋.面向空间数据组织的地理空间剖分框架性质分析
[J].北京大学学报:自然科学版,2012,48(1):123132.
[9] CramptonJW,GrahamM,PoorthuisA,etal.Beyondthegeotag:situ
ating‘bigdata’andleveragingthepotentialofthegeoweb[J].Car
tographyandGeographicInformationScience,2013,40(2):
130139.
[10]WagnerHH,FortinMJ.Aconceptualframeworkforthespatialanalysisoflandscapegeneticdata[J].ConservationGenetics,2013,14(2):253261.
[11]陈江平,黄炳坚.数据空间自相关性对关联规则的挖掘与实验分析[J].地球信息科学学报,2011,13(1):109117.
[12]AnselinL,SyabriI,KhoY.GeoDa:anintroductiontospatialdataanalysis[R]//HandbookofAppliedSpatialAnalysis.Berlin:Springer,2010:7389[13]ReySJ,AnselinL.PySAL:apythonlibraryofspatialanalyticalmethods[R]//HandbookofAppliedSpatialAnalysis.Berlin:Springer,2010:175193.



